Convex Hull

There are multiple trees growing in a garden, each with a distinct (x, y) coordinate. You are tasked to enclose all of these trees with a single rope. The amount of rope you use should be minimised. Find the coordinates of the trees located along the rope.

Note: The garden has at least one tree and the points you’re given have no order. You’re not required to sort your output either.
Input:  [[1, 1], [2, 2], [2, 0], [2, 4], [3, 3], [4, 2]]
Output: [[1, 1], [2, 0], [4, 2], [3, 3], [2, 4]]

Our objective is to build the shortest perimeter that can contain all input coordinates. This perimeter is more formally known as a convex hull.

There are a variety of methods you can use to build a convex hull. These include Graham’s scan and Jarvis’ march (also known the Gift Wrapping algorithm). To implement them, you’ll need to have some knowledge of concepts such as polar angles and vector cross products. The following MIT lecture covers yet another alternative –– the divide-and-conquer approach:

My initial plan was to dive into the textbook version of Graham’s scan, but I encountered this elegant solution written by sberens that 1) bore some resemblance to Graham’s scan and 2) struck me as being easier to understand. Let’s explore this approach in detail.

Selecting a Starting Point

Suppose that the garden in our problem statement has trees (which I’ll refer to as nodes from this point) at the following positions:

Garden of trees labelled 'A', 'B', 'C', 'D', 'E', 'F' and 'G'.

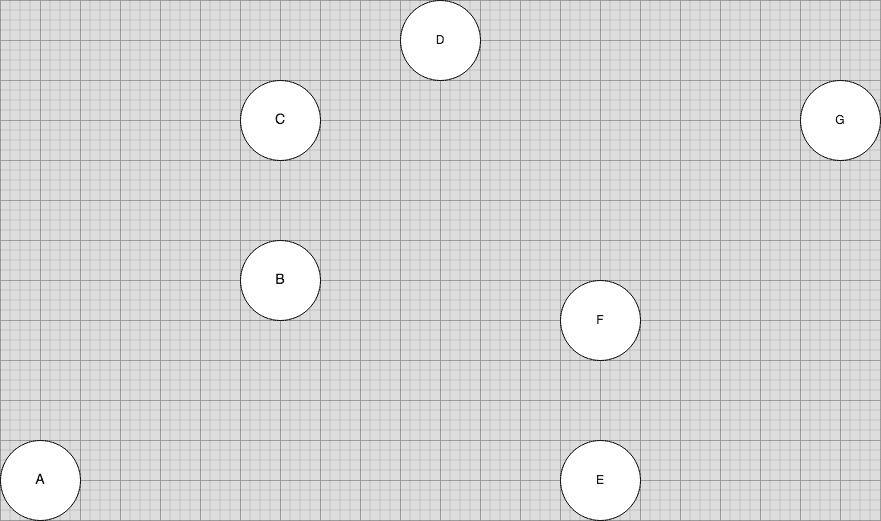
Intuitively, we’ll want to evaluate each node, one at a time, to see if it belongs to the convex hull. Where do we begin?

It seems fair to say that nodes at the boundaries must belong to the convex hull. Nodes that fall in this group would include 'A', 'D', 'E', and 'G' –– as they possess either minimum or maximum values along the x and / or y axes. For simplicity, let’s start with 'A', our leftmost node.

Before we begin traversing the garden, we’ll need a framework for determining each node’s viability for being included in the hull.

Properties of Convex Hulls

Let’s outline the actual convex hull for this garden and see if we can identify some properties associated with it.

Convex hull consisting of nodes 'A', 'C', 'D', 'E', and 'F'.

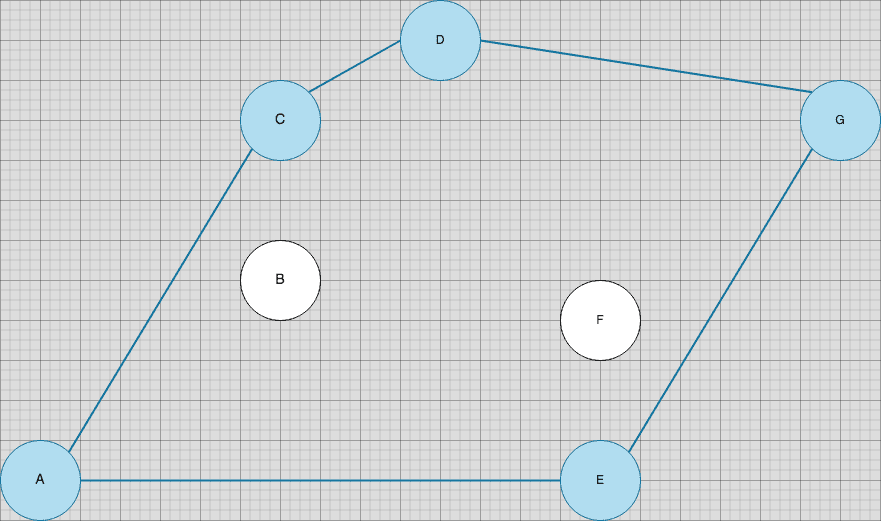
Consider the gradients of the line segments formed by the pairs of nodes that constitute the upper portion of the convex hull ('A' to 'C', 'C' to 'D', and 'D' to 'G'). Notice that these gradients are strictly non-increasing.

Similarly, consider the gradients of the line segments formed by the pairs of the nodes that constitute the lower portion of the convex hull ('A' to 'E' and 'E' to 'G'). These gradients appear to be strictly non-decreasing.

These two properties we’ve observed turn out to be key in helping us identify convex hull nodes!

For example, it cannot be the case that the line segments connecting 'A' to 'B' and 'B' to 'C' make up the convex hull. The gradient of the latter is larger than that of the former, and we can immediately see that more suitable line segment can be drawn between 'A' and 'C':

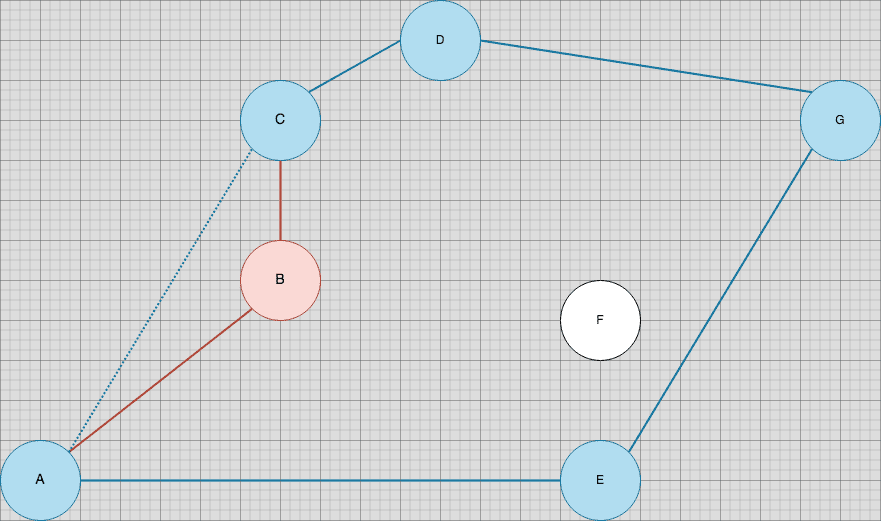
In other words, we now have two invariants that we’ll need to enforce:

Line segments which form the upper portion of the convex hull should have a non-increasing gradient
Line segments which form the lower portion of the convex hull should have a non-decreasing gradient

We’ll refer to the corresponding two sequences of nodes as the upper and lower chains.

Navigating the Garden

We’ve yet to establish an order for visiting the rest of the nodes. Since we’re starting from the lowest node on our left boundary, it seems natural to scan the garden from left to right. For nodes that share that same x value, we’ll visit them from bottom to top (both ways work fine as long we handle the signs on the infinite gradients).

The primary data structure we’ll be using here is a stack that stores the chain of nodes we’ll eventually return. Suppose we’re moving through the garden and we’ve visited nodes 'A' to 'E'. We’ve stored nodes 'A', 'C', 'D' and 'E' in our stack (dropping 'B' along the way) and we’re now evaluating 'F' as a candidate:

Evaluating the candidacy of 'F' as a convex hull node.

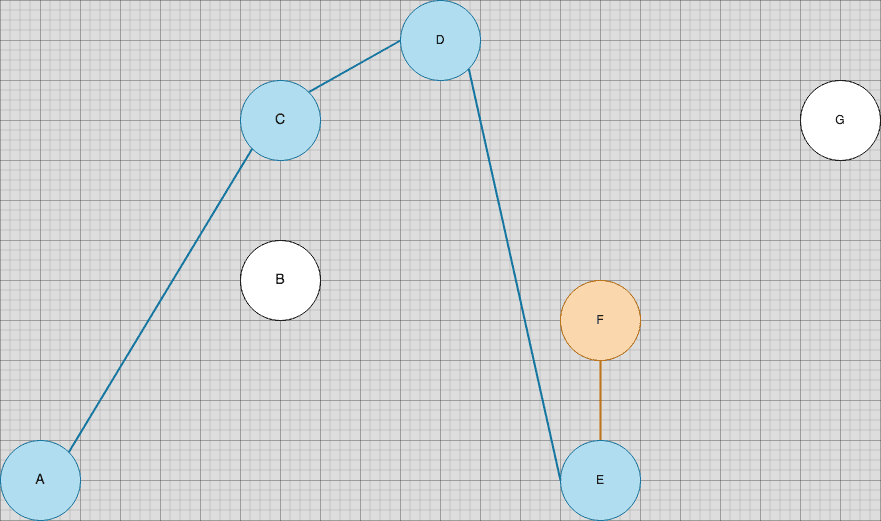
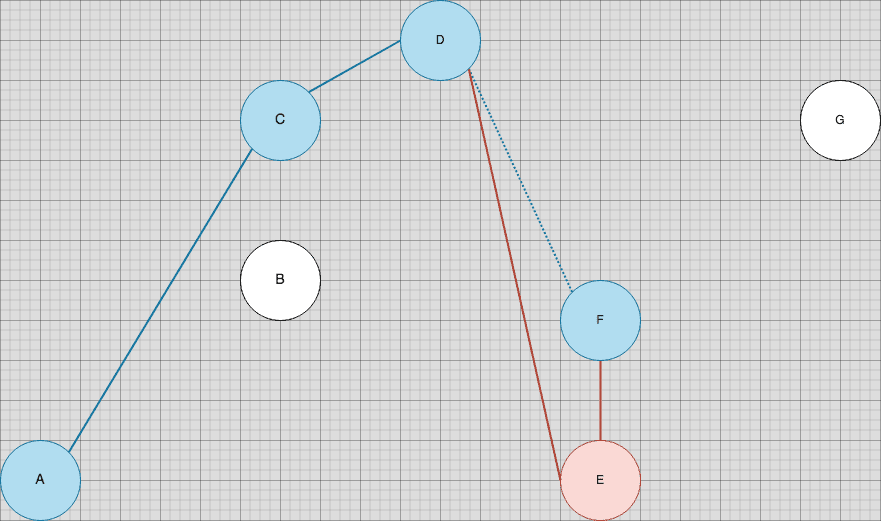
To enforce the invariant we described earlier, we’ll want to check the gradient of 'D' (the next-to-top item in our stack) to 'E' (the top item in our stack) against the gradient of 'E' (the top item in our stack) to 'F' (the incoming item).

Clearly, the gradient increase violates the non-increasing invariant we defined earlier, so we’ll dismiss 'E' from the stack by popping it off and replacing it with 'F':

Popping 'E' off the stack and appending 'F'.

Subsequently, when we inspect 'G', we’ll see the invariant being violated again. The gradient of 'F' to 'G' is greater than the gradient of 'D' to 'F', so we’ll replace 'F' with 'G' in our stack.

Evaluating the candidacy of 'G' as a convex hull node.

Popping 'F' off the stack and appending 'G'.

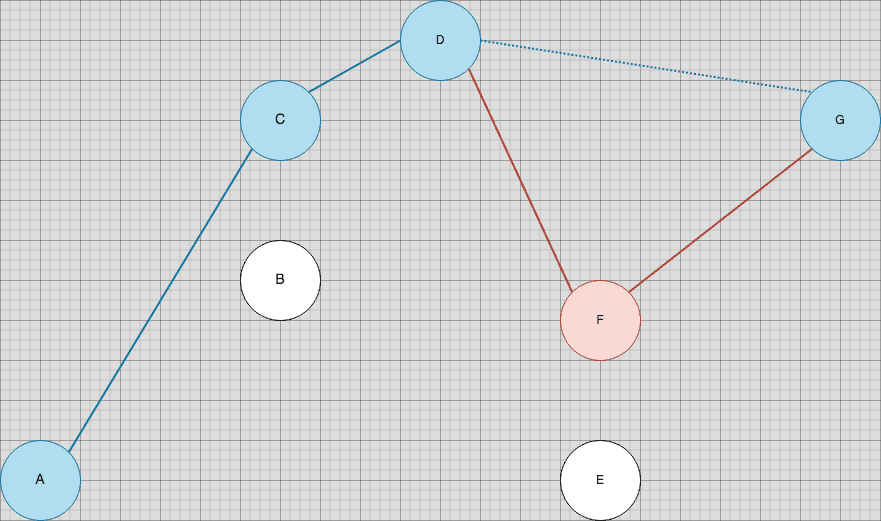
This completes the upper chain of our convex hull.

You can imagine this process being repeated another time in order for us to derive the lower chain. The only difference, in this second iteration, is that we’ll be enforcing the non-decreasing invariant instead.

From Intuition to Code

First, let’s define a helper for computing gradients, since we’ll be comparing them extensively:

def g(ref, p):
    numerator = p[1] - ref[1]
    denominator = p[0] - ref[0]
    if denominator == 0:
        return math.inf
    return fractions.Fraction(numerator, denominator)

We’ll also define another helper for the chaining algorithm we described earlier:

def build_chain(comp):
    chain = [points[0]]
    for p in points[1:]:
        while (
            len(chain) >= 2 and
            # Compare the previous gradient to the incoming
            # gradient. If we detect a violation, pop the
            # last node in our chain.
            comp(
                g(chain[-2], chain[-1]),
                g(chain[-1], p)
            )
        ):
            chain.pop()
        chain.append(p)
    return chain

We enforce the invariant through the use of a function that’s passed as a parameter, comp. At call sites, comp will either be passed as operator.lt or operator.gt. We do this for reusability benefits, because we’ll have to traverse the garden twice and enforce the invariants both ways (non-decreasing and non-increasing).

With these two helpers, putting together the convex hull algorithm becomes trivial:

def g(ref, p):
    # ...

def outer_trees(points):
    # Minor optimisation
    if len(points) <= 3:
        return points

    def build_chain(comp):
        # ...

    points.sort()
    topchain = build_chain(operator.lt)
    btmchain = build_chain(operator.gt)
    # De-duplicate points in both chains
    return set([tuple(p) for p in topchain + btmchain])

Recall that our inputs are not guaranteed to have an sorting order, so we sort them before building the upper and lower chains.

The last line of our code is worth highlighting. We de-duplicate nodes because the node subsets representing our upper and lower chains will overlap. For instance, in the example above, you can imagine the first node ('A') and the last node ('G') of both chains being the same. In certain edge cases (such as if the garden was composed of nodes in a straight line with gradients of zero), you would have more overlaps.

Given n trees in the garden, our algorithm runs in O(n) space and O(n log n) time.

With that, we’ve solved the Convex Hull problem 🧱🌳🌳🧱.

Full Solution

import math
import fractions


def g(ref, p):
    numerator = p[1] - ref[1]
    denominator = p[0] - ref[0]
    if denominator == 0:
        return math.inf
    return fractions.Fraction(numerator, denominator)


def outer_trees(self, points):
    # Minor optimisation
    if len(points) <= 3:
        return points

    def build_chain(comp):
        chain = [points[0]]
        for p in points[1:]:
            while (
                len(chain) >= 2 and
                # Compare the previous gradient to the incoming
                # gradient. If we detect a violation, pop the
                # last node in our chain.
                comp(
                    g(chain[-2], chain[-1]),
                    g(chain[-1], p)
                )
            ):
                chain.pop()
            chain.append(p)
        return chain

    points.sort()
    topchain = build_chain(operator.lt)
    btmchain = build_chain(operator.gt)
    # De-duplicate points in both chains
    return set([tuple(p) for p in topchain + btmchain])

Published 27 Feb 2020

Thanks for reading! If you gained something from reading this article, feel free to tweet about it or share your thoughts in the comments section below 💬.