Huffman Coding

From EPI:

Given a set of characters and their corresponding frequencies of occurrence, produce Huffman codes for each character such that the average code length is minimised. Return the average code length.

Note: Huffman codes are prefix codes –– one code cannot be a prefix of another. For example, "011" is a prefix of "0110" but not a prefix of "1100".

Note: The average code length is defined to be the sum of the product of the length of each character’s code word with that character’s frequency.
Input: [
    ["a", 8.167], ["b", 1.492], ["c", 2.782], ["d", 4.253],
    ["e", 12.702], ["f", 2.228], ["g", 2.015], ["h", 6.094],
    ["i", 6.966], ["j", 0.153], ["k", 0.772], ["l", 4.025],
    ["m", 2.406], ["n", 6.749], ["o", 7.507], ["p", 1.929],
    ["q", 0.095], ["r", 5.987], ["s", 6.327], ["t", 9.056],
    ["u", 2.758], ["v", 0.978], ["w", 2.36], ["x", 0.15],
    ["y", 1.974], ["z", 0.074]
]

Output: 4.205019999999999

The Huffman coding algorithm is a fairly well-known method for compressing information in a lossless manner. Suppose you’re given a payload containing some symbols and you’d like to compress this payload into the smallest possible number of bits. Intuitively, you’d want a way to:

Map each symbol to a specific sequence of bits
Use fewer bits for symbols that occur more frequently, and vice versa

In this problem, we’re already given the list of symbols and their respective frequencies, so we don’t have to trouble ourselves with figuring out this metadata:

# Each element in `symbols` is a tuple in the form of: 
CharWithFrequency = collections.namedtuple(
    'CharWithFrequency', ('c', 'freq')
)

def huffman_encoding(symbols):
    # ...

That said, it’s reasonable to expect a variant of this problem where you’re given a string "aaccbbcc" and asked to calculate the frequencies for each symbol yourself. A symbol’s (or in this case, a character’s) frequency is simply a percentage value of the number of occurrences over the size of the input.

def get_char_with_frequencies(s):
    ctr = collections.Counter(s)
    symbols = []
    for char in ctr:
        symbols.append(CharWithFrequency(
            char, (ctr[char] / len(s)) * 100
        ))
    return symbols

get_char_with_frequencies("aaccbbcc") 
# [
#     CharWithFrequency(c='a', freq=0.25),
#     CharWithFrequency(c='c', freq=0.5),
#     CharWithFrequency(c='b', freq=0.25)
# ]

Selecting Bits for a Huffman Code

The Huffman coding algorithm requires us to construct a binary tree that will capture the prefix codes for all given symbols. Every edge in this binary tree represents a choice between a '0' or '1' bit. Every leaf node embodies a unique symbol.

Depiction of a Huffman tree with 3 symbols.

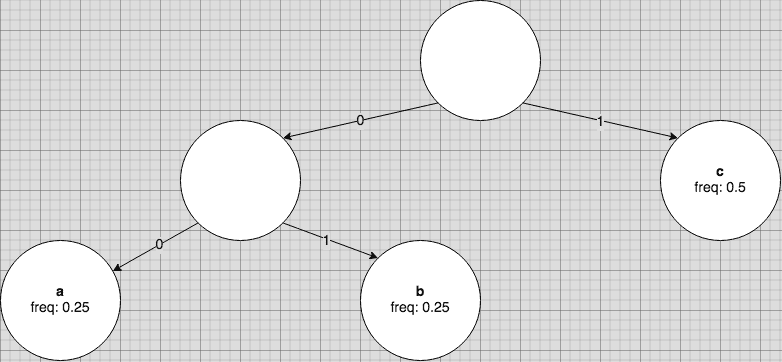
A path in the binary tree from root to leaf describes the code for a symbol. For instance, the code for 'b' in the above tree would be '01', since we traverse through '0' and '1' before reaching the associated leaf node:

The path leading to the character 'b' is 0 -> 1, so its Huffman code must be "01".

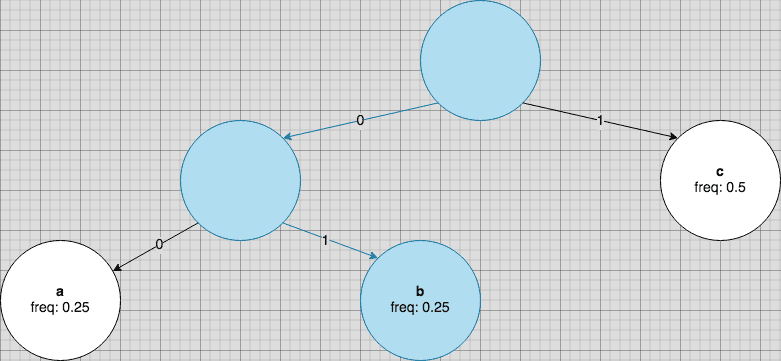
The properties of this binary tree guarantee that all prefix codes will be valid. Since the nodes representing symbols are all leaves, none of the symbols are ancestors of other symbols, so it cannot be that one code is a prefix of another.

Building the Huffman Tree

Of course, this raises the question –– how do we construct a Huffman tree? Let’s start by defining the structure of our nodes:

class Node:
    def __init__(self, c=None, freq=None):
        self.c = c  # Character
        self.freq = freq  # Frequency
        self.left = self.right = None

    def __lt__(self, other):
        return self.freq < other.freq

We’ll organise these nodes into a min-heap based priority queue so that we can greedily pop pairs of nodes with the lowest frequencies. We’ll then create a parent node that combines these pairs into a single subtree and insert this subtree into the queue:

# Store symbols as nodes, heapify nodes
q = []
for cwf in symbols:
    heapq.heappush(q, (cwf.freq, Node(cwf.c, cwf.freq)))

# Bottom-up construction of Huffman tree 
# Pop nodes / subtrees in pairs and combine them
while len(q) >= 2:
    node1 = heapq.heappop(q)[1]
    node2 = heapq.heappop(q)[1]
    node3 = Node(c=None, freq=node1.freq + node2.freq)
    node3.left = node1
    node3.right = node2
    heapq.heappush(q, (node3.freq, node3))

Why do we begin with the nodes that have the lowest frequencies?

Consider the fact that our algorithm combines subtrees into larger subtrees and turns those subtrees into even larger ones. By starting with the lowest frequency nodes, we ensure that these nodes will be furthest from the root.

By extension, doing this ensures that the highest frequency nodes will be closest to the root. We want this because symbols that occur most frequently should have the shortest Huffman codes:

The character 'c' occurs at a higher frequency compared to the characters 'a' and 'b' –– so we want its distance to the root to be shorter.

As we repeatedly process pairs of nodes, you can imagine our queue shrinking from a size of n to a size of n-1, n-2, n-3, and all the way to 1. The final node in our queue (i.e. q[0]) will be the root of our binary tree.

Computing the Average Code Length

Once the tree has been constructed, we’ll want to traverse it to derive the actual Huffman codes for each symbol. A simple DFS will suffice:

# Generate codewords
codewords = {}
def DFS(node, acc_code):
    if not node:
        return None
    if node.c:
        codewords[node.c] = (acc_code, node.freq)
    DFS(node.left, acc_code + '0')
    DFS(node.right, acc_code + '1')
DFS(q[0][1], '')

Having defined the mappings between symbols and their respective Huffman codes, we can proceed to calculate the average code length for each symbol. We’ll multiply the length of each code by its frequency (in percentage terms) and sum the values across all symbols.

res = 0
for char in codewords:
    code, freq = codewords[char]
    res += (freq / 100) * len(code)
return res

Given n symbols, our algorithm runs in O(n) space and O(n log n) time.

With that, we’ve solved the Huffman Coding problem 🔠📜🔢.

Full Solution

class Node:
    def __init__(self, c=None, freq=None):
        self.c = c  # Character
        self.freq = freq  # Frequency
        self.left = self.right = None

    def __lt__(self, other):
        return self.freq < other.freq


def huffman_coding(symbols):
    # Store symbols as nodes, heapify nodes
    q = []
    for cwf in symbols:
        heapq.heappush(q, (cwf.freq, Node(cwf.c, cwf.freq)))

    # Bottom-up construction of Huffman tree 
    # Pop nodes / subtrees in pairs and combine them
    while len(q) >= 2:
        node1 = heapq.heappop(q)[1]
        node2 = heapq.heappop(q)[1]
        node3 = Node(c=None, freq=node1.freq + node2.freq)
        node3.left = node1
        node3.right = node2
        heapq.heappush(q, (node3.freq, node3))

    # Generate codewords
    codewords = {}
    def DFS(node, acc_code):
        if not node:
            return None
        if node.c:
            codewords[node.c] = (acc_code, node.freq)
        DFS(node.left, acc_code + '0')
        DFS(node.right, acc_code + '1')
    DFS(q[0][1], '')

    # Calculate avg code length
    res = 0
    for char in codewords:
        code, freq = codewords[char]
        res += (freq / 100) * len(code)
    return res

Published 26 Feb 2020

Thanks for reading! If you gained something from reading this article, feel free to tweet about it or share your thoughts in the comments section below 💬.