
I recently had the pleasure of reading a great article by Ilija Eftimov.
It covers how LFU caches may be applied in practice and explains how their operations can be handled in constant time. The algorithm is derived from a 2010 paper and I highly recommend checking it out.
At present, modern web browsers rely on LRU as an eviction policy. It’s not too far-fetched to imagine that these platforms might one day revisit the idea of using an alternative mechanism, such as LFU, for certain subsets of cached data.
Requirements
To support constant time LFU operations, we’ll need a few simple data structures:
-
A doubly linked list of frequency nodes (
FreqNode), where each node represents a frequency key. -
A doubly linked list of data nodes (
DataNode), where each node represents a data value for a given data key. -
A map (or hashmap) of data keys to data values (
lfu.data_nodes).
The following diagram depicts what an LFU cache might look like, once we bring these data structures together:
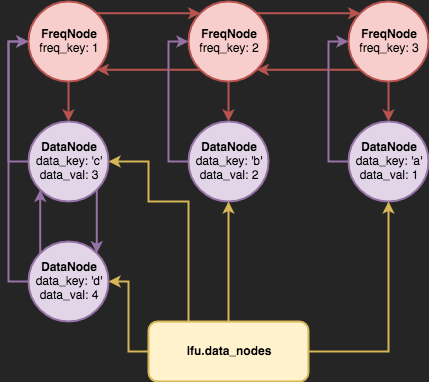
Some key points worth mentioning:
-
Every
FreqNodehas its own associated list of data nodes. When an existing data node is accessed either viaputorget, it gets “promoted” from one frequency node to another. The time complexity of removing a node from a linked list and adding it to another is O(1). -
If a
DataNodeis promoted from oneFreqNodeto another but the latter doesn’t exist, we’ll splice in a newFreqNodeto represent the incremented frequency. -
lfu.data_nodes, the hashmap, allows us to quickly access any of our data items in O(1) time.
Setup
Let’s start defining the data structures that will constitute our LFU cache.
Defining Node Classes
For starters, we’ll define two node types. We’ll need one class to represent frequencies:
class FreqNode:
def __init__(self, freq_key):
self.prev = self.next = None
self.freq_key = freq_key
self.data_list = LinkedList()And we’ll need another class to represent the actual data –– the key-value pairs we’re storing:
class DataNode:
def __init__(self, data_key, data_val, freq_node):
self.prev = self.next = None
self.data_key = data_key
self.data_val = data_val
self.freq_node = freq_node
Both of these node types will serve as building blocks for the doubly linked lists in our LFU cache.
Defining a Doubly Linked List
Since Python doesn’t have built-in support for doubly linked lists, we’ll have to write our own:
class LinkedList:
def __init__(self):
self.head = self.tail = None
self.size = 0
def append(self, node):
if self.size == 0:
self.head = self.tail = node
else:
self.tail.next = node
node.prev = self.tail
self.tail = node
self.size += 1
def prepend(self, node):
if self.size == 0:
self.head = self.tail = node
else:
self.head.prev = node
node.next = self.head
self.head = node
self.size += 1
def insert_after(self, ref_node, node):
ref_node_next = ref_node.next
# Connect ref_node to node
ref_node.next = node
node.prev = ref_node
# Connect node to ref_node_next
node.next = ref_node_next
if ref_node_next:
ref_node_next.prev = node
if self.tail is ref_node:
self.tail = node
self.size += 1
def remove(self, node):
if self.tail is node:
self.tail = node.prev
if self.head is node:
self.head = node.next
# Connect adj nodes
if node.prev:
node.prev.next = node.next
if node.next:
node.next.prev = node.prev
# Isolate node
node.next = node.prev = None
self.size -= 1A few things to note here:
-
We include a
linked_list.insert_after()method so that it’ll be easy to splice in frequency nodes -
linked_list.remove()can potentially cause problems if it isn’t used carefully. This is because the method doesn’t verify if the node to remove actually exists in thelinked_listinvoking it.
With these data structures in place, we can start defining our LFU cache.
Writing the LFU Cache
An LFU cache takes in a single param, capacity, which dictates the number of data key-value pairs which can be stored in it.
lru.data_nodes stores the mappings for every key-value pair, while lru.freq_list maintains the range of frequencies for all existing keys.
class LFUCache:
def __init__(self, capacity):
self.data_nodes = {}
self.freq_list = LinkedList()
self.capacity = capacityWhenever put or get is called for a given data node, we’ll need to increment its frequency. We should flesh out the logic for this subroutine first:
class LFUCache:
def increment_freq(self, data_node):
freq_node = data_node.freq_node
freq_key = freq_node.freq_key
# Check if next frequency key exists
if not (
freq_node.next and
freq_node.next.freq_key == freq_key + 1
):
self.freq_list.insert_after(
freq_node, FreqNode(freq_key=freq_key+1)
)
# Remove data_node from freq_node's data_list
# Add data_node to next_freq_node's data_list
freq_node.data_list.remove(data_node)
freq_node.next.data_list.append(data_node)
# Update data_node's own internal reference
data_node.freq_node = freq_node.next
# If the freq_node's data_list has been
# trimmed to zero, we remove it from the freq_list
if freq_node.data_list.size == 0:
self.freq_list.remove(freq_node)Now we’re ready to handle the main LFU operations. lfu.put() is more difficult to handle than lfu.get() as it requires us to check if our LFU’s capacity has reached its limit.
Note that identifying the node to remove is a constant time operation –– we can look up the head frequency node and remove the head data node associated with it.
class LFUCache:
def put(self, data_key, data_val):
# Key already exists, simply update
if data_key in self.data_nodes:
data_node = self.data_nodes[data_key]
self.increment_freq(data_node)
data_node.data_val = data_val
return
# Key doesn't exist, we need to insert a new one
# Remove outdated nodes if necessary
if len(self.data_nodes) == self.capacity:
# Edge case: Capacity == 0, do nothing
if self.capacity == 0:
return
# Find removable node
lowest_data_list = self.freq_list.head.data_list
rem_node = lowest_data_list.head
lowest_data_list.remove(rem_node)
del self.data_nodes[rem_node.data_key]
# Delete data_list if necessary
if lowest_data_list.size == 0:
self.freq_list.remove(self.freq_list.head)
# Add new node
# Create new freq_node if necessary
if not (
self.freq_list.head and
self.freq_list.head.freq_key == 1
):
self.freq_list.prepend(FreqNode(1))
# Create new data_node and add it with a key of 1
new_data_node = DataNode(
data_key=data_key,
data_val=data_val,
freq_node=self.freq_list.head
)
self.freq_list.head.data_list.append(new_data_node)
self.data_nodes[data_key] = new_data_nodeThe code for lfu.get() pretty straightforward, since it only entails reading data values (if they exist):
class LFUCache:
def get(self, data_key):
# Key exists, assign it to a next freq_node
if data_key in self.data_nodes:
self.increment_freq(self.data_nodes[data_key])
return self.data_nodes[data_key].data_val
else:
return -1Concluding Thoughts
In a certain sense, you can think of an LFU cache as an unconventional way of representing a sorted collection. Python’s collections.OrderedDict bears a bit of similarity and is, in fact, perfect for __LRU__s!
There are, of course, limitations with this implementation. For instance, we can’t insert a new DataNode with a key larger than 1 –– it’s not like we can bisect the frequency nodes and preserve our O(1) performance. Nevertheless, taken as a whole, an O(1) LFU is surely a welcome addition to any developer’s arsenal of data structures.